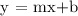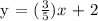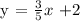Question

6.Write the equation in slope-intercept form for the line that passes through the given pointand is perpendicular to the given equation.5x + 3y = -21 and passes through (-5, 1)

Answer 1

Let us first solve for the slope (m) of the perpendicular line.

`\text{ 5x + 3y = -21}`
`\text{ 3y = -5x - 21}`
`\text{ y =}\frac{-5x\text{ -21}}{3}`
`\text{ y = -}(5)/(3)x-7`

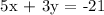
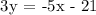
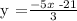
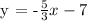
The slope of the perpendicular line is -5/3.

Thus, for the slope of the line, we get,

`\text{ m}_(\perp)\text{ = }(-5)/(3)`
`\text{ m = }(3)/(5)`

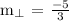
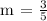
Let us solve for the value of b with the given value of slope (m) = 3/5 and (x,y) = (-5,1).

`\text{ y = mx + b}`
`1\text{ = (}(3)/(5))(-5)+b`
`1\text{ = -1 + b ; b = 1 + 1 = }2`

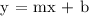
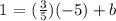
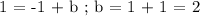
Let's now make the equation of the line using Slope-Intercept Form,

Given, m = 3/5 and b = 2

`\text{ y = mx+b}`
`\text{ y = (}(3)/(5))x\text{ + 2}`

`\text{ y = }(3)/(5)x\text{ +2}`