Question

If x equals negative 2 and y equals the square root of 12, then begin expression . . . 2 times the quantity . . . 3 times x raised to the third power, plus 2 times y raised to the second power . . . end expression . . . equals

Answer 1

I don't understand your question, expressions do not end with equal signs. Or are you just asking how to write the expression?

2*((3*x)^3)+2(y^2) then simply replace the x with "-2" and y with "sqrt(12)"
2*(-2)^3+2(12)
-16+24
8

Answer 2

The value of given expression at x = -2 and y =
`√(12)` is 0

Explanation:Given expression : 2 times the quantity 3 times x raised to the third power, plus 2 times y raised to the second power .

WE have to evaluate the value of given expression at x equals negative 2 and y equals the square root of 12 that at x = -2 and y =
`√(12)`

Given expression can be represented mathematically as,

`2(3x^3+2y^2)`

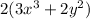
First we simplify the given expression,

`\Rightarrow 2(3x^3+2y^2)`

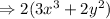
Put x = -2 and y =
`√(12)` , we get

`\Rightarrow 2(3(-2)^3+2(√(12))^2)`

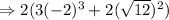
On simplifying, we get,

`\Rightarrow 2(3(-8)+2(12)`

`\Rightarrow 2(-24+24)`

`\Rightarrow 2(0)`

`\Rightarrow 0`

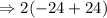
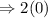
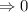
Thus, the value of given expression at x = -2 and y =
`√(12)` is 0