Answer:
Option A and B are correct.
Explanation:
Two vertices of a right triangle are located at A(1, 3) and B(2, 5)
We have to choose the third vertex from the options. We have to check each option.
Using Distance formula:
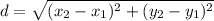
Pythagorous Identity:
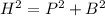
We will find the length of each side and then apply pyhtagoreous property.
If Pythagorean theorem follow then it could be third vertex else not
Option A: C(1,5)
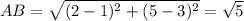
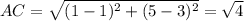
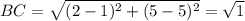
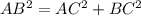
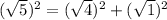

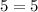
TRUE
Option B: C(2,3)
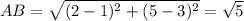
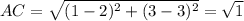
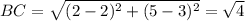
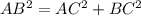
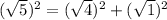

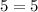
TRUE
Option C: C(3,3)
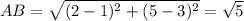
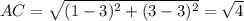
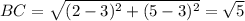
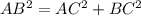
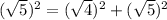
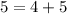

FALSE
Option D: C(3,5)
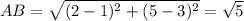
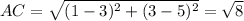

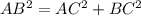
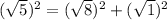
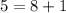

FALSE