Question

Which of the following represents the zeros of f(x) = x3 − 3x2 − 2x + 6?

A.) −3, −√2, −√2
B.) 3, −√2, −√2
C.) −3, √2, √2
D.) 3, √2, −√2

Answer 1

D. {3, √ 2, -√ 2}.
The cubic factors- (x - 3)(x² - 2) = 0.

Answer 2

Answer:D.) 3, √2, −√2

Explanation:

Given polynomial:
`f(x)=x^3-3x^2-2x+6`

Let's check all the given options, by substituting given value on x.

A.) −3, −√2, −√2

`f(-3)=(-3)^3-3(-3)^2-2(-3)+6=-27-27+6+6=-42\\eq 0`

⇒ -3 is not a zero of given polynomial.

Thus, this not the required answer.

B.) 3, −√2, −√2

`f(3)=(3)^3-3(3)^2-2(3)+6=27-27-6+6=0`

`f(-√(2))=(-√(2))^3-3(-√(2))^2-2(-√(2))+6\\\\=-2√(2)-6+2√(2)+6=0`

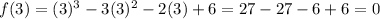
But by Descartes rule of sigs , f(x) have 2 positive and 1 negative root.

Thus, this is not the right answer.

C.) −3, √2, √2

-3 is not a zero of given polynomial.

Thus, this not the required answer.

D.) 3, √2, −√2

`f(-3)=(-3)^3-3(-3)^2-2(-3)+6=-27-27+6+6=-42\\eq 0`

`f(√(2))=(√(2))^3-3(√(2))^2-2(√(2))+6\\\\=2√(2)-6-2√(2)+6=0`

`f(-√(2))=(-√(2))^3-3(-√(2))^2-2(-√(2))+6\\\\=-2√(2)-6+2√(2)+6=0`

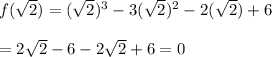
Thus, this is the right option to have zeroes of f(x).