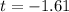Answer:
The value of the test statistic is
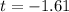
Explanation:
Central Limit Theorem
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
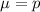 and standard deviation
and standard deviation
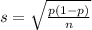
Our test statistic is:
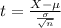
In which X is the sample mean,
 is the expected mean,
is the expected mean,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
A publisher reports that 52% of their readers own a laptop.
This means that
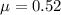
Sample of 180:
Means that
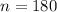
By the Central Limit Theorem:

A random sample of 180 found that 46% of the readers owned a laptop.
This means that

Find the value of the test statistic.
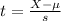
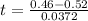
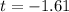
The value of the test statistic is