Answer:
a)
Mass flow rate of core =
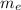 = 60.94 Kg/s
= 60.94 Kg/s
Mass flow rate of fan =
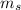 = 73.12 kg/s
= 73.12 kg/s
TSFC = 3.301 x
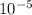
b)
Exit Area of Fan =
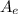 = 0.3624
= 0.3624

Exit Area of Core =
 = 0.2635
= 0.2635

Step-by-step explanation:
Data Given:
Height = 25000 ft
Vehicle velocity =
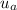 = 815 ft/s = 248.41 m/s
= 815 ft/s = 248.41 m/s
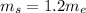
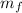 = 0.0255
= 0.0255
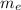
Where,
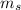 = Mass flow rate of fan
= Mass flow rate of fan
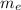 = Mass flow rate of core
= Mass flow rate of core
F = Thrust
Density of core =
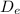 = 0.000578 slugs/
= 0.000578 slugs/
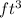 = 0.2979 kg/
= 0.2979 kg/

Density of fan =
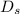 = 0.00154 slugs/
= 0.00154 slugs/
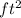 = 0.7937 kg/
= 0.7937 kg/

Ambient Pressure of Fan =
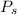 = 10.07 Psi = 69430.21 Pa
= 10.07 Psi = 69430.21 Pa
Ambient Pressure of core =
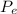 = 10.26 Psi = 70740.2 Pa
= 10.26 Psi = 70740.2 Pa
Thrust = F = 10580 lbf = 47062.2 N
Velocity of fan =
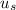 = 1147 ft/s = 349.6 m/s
= 1147 ft/s = 349.6 m/s
Velocity of core =
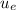 = 1852 ft/s = 564.5 m/s
= 1852 ft/s = 564.5 m/s
At the height of 25000 ft, P = 37600
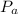
Now,
we have:
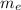 =
=
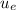 x
x
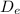 x
x
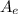
Plugging in the values, we get:
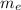 = 168.16
= 168.16
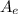 Equation 1
Equation 1
And,
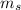 =
=
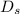 x
x
 x
x
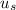
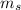 = 277.5
= 277.5
 Equation 2
Equation 2
As, we know,
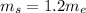
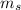 = 277.5
= 277.5

And now for Thrust, we have:
F =
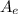 x (
x (
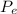 -
-
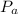 ) +
) +
 x (
x (
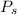 -
-
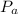 ) +
) +
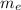 x (
x (
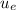 -
-
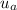 ) +
) +
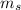 x (
x (
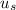 -
-
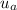 ) Equation 3
) Equation 3
Now, substitute equation 1 and 2 in equation 3, we get:
Exit Area of Fan =
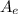 = 0.3624
= 0.3624

Exit Area of Core =
 = 0.2635
= 0.2635

Mass flow rate of core =
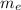 = 60.94 Kg/s
= 60.94 Kg/s
Mass flow rate of fan =
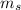 = 73.12 kg/s
= 73.12 kg/s
TSFC = Thrust Specific Fuel Consumption = fuel mass flow rate / Thrust
TSFC =
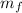 /F
/F
And,
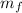 = 0.0255
= 0.0255
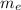
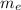 = 60.94
= 60.94
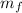 = 0.0255 x 60.94
= 0.0255 x 60.94
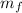 = 1.55397
= 1.55397
TSFC =
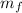 /F
/F
TSFC = 1.55397/47062.2
TSFC = 3.301 x
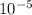
Low TSFC = High efficiency
High TSFC = Low efficiency
a)
Mass flow rate of core =
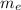 = 60.94 Kg/s
= 60.94 Kg/s
Mass flow rate of fan =
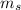 = 73.12 kg/s
= 73.12 kg/s
TSFC = 3.301 x
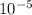
b)
Exit Area of Fan =
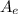 = 0.3624
= 0.3624

Exit Area of Core =
 = 0.2635
= 0.2635
