Question

If the vertex of a Parabola is (-4,6) and another point of the curve is (-3, 14) what is the coefficient of the squared expression in the parabola's equation?

Answer 1

`\bf \qquad \textit{parabola vertex form} \\\\\\ y=a(x-{{ h}})^2+{{ k}}\\ x=a(y-{{ k}})^2+{{ h}}\qquad\qquad vertex\ ({{ h}},{{ k}})`

so.. based on the provided points, we can more or less make that is a vertical parabola, so "x" is the squared variable, so we'll use the 1st of the above ones


`\bf y=a(x-{{ h}})^2+{{ k}}\qquad \begin{cases} vertex\ (-4,6)\to \begin{cases} h=-4\\ k=6 \end{cases}\\\\\\ \textit{another point}\\ (-3,14)\to \begin{cases} x=-3\\ y=14 \end{cases} \end{cases} \\\\\\ y=a(x-(-4))^2+6\implies y=a(x+4)^2+6\impliedby \textit{what's`

solve for "a"

Answer 2

Answer: The coefficient of squared expression is,

`8\text{ or } -(1)/(36)`

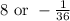
Step-by-step explanation:

There can be two cases,

Case 1 : If the parabola is along y-axis,

Since, the standard equation of parabola along y-axis is,

`y=a(x-h)^2+k`

Where, (h,k) is the vertex of the parabola,

Here, (h,k) = (-4,6),

By substituting the values,

`y=a(x-(-4))^2+6`

`y=a(x+4)^2+6`

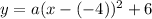
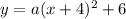
Given, another point of the parabola is (-3, 14),

⇒ (-3, 14) must satisfy the above equation,

`14=a(-3+4)^2+6`

`14=a+6`

`\implies a=8`

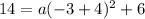
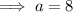
Hence, the coefficient of squared expression is 8.

Case 2 : If the parabola is along x-axis,

The standard equation of parabola along x-axis is,

`x=a(y-h)^2+k`

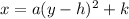
Where, (h,k) is the vertex of the parabola,

Here, (h,k) = (-4,6),

By substituting the values,

`x=a(y-(-4))^2+6`

`x=a(y+4)^2+6`

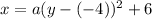
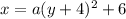
Given, another point of the parabola is (-3, 14),

⇒ (-3, 14) must satisfy the above equation,

`-3=a(14+4)^2+6`

`-3-6=a(18)^2`

`-9=324 a`

`\implies a=-(9)/(324)=-(1)/(36)`

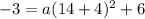
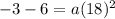
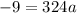
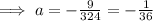
Hence, the coefficient of squared expression is -1/36.