Question

A fisherman traveled in a boat from point N upstream. After having traveled 6 km, he stopped rowing and 2 hour 40 min after first leaving N, he was brought back to N by the current. Knowing that the speed of the boat in still water is 9 km/hour, find the speed of the river’s current.

Answer 1

so.. the boat in still water runs at 9km/h, so that's its rate

going from N upstrea, going against the current's rate, you guessed it, if the stream has a rate "r", then the boat is going up at 9 - r

now, he started out at point N, and stop rowing, and backslid to point N
the way back he was just going at the current's speed or "r"

notice, he started from point N, went up 6km, then came back to point N, meaning, the distance one way is 6km, and back is the same 6km

now, since he started from point N, till he came back, the length of the whole trip forth and back is 2hrs and 40mins, or 160minutes

well, you know that d = rt
thus
`\bf \begin{array}{lccclll} &distance(km)&rate(kmph)&time(minutes)\\ &-----&-----&-------\\ \textit{from N}&6&9-r&t\\ \textit{back to N}&6&r&160-t \end{array}`

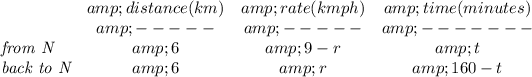
I'd think you know how to get "r" by now

Answer 2

Answer: 4.5 km/h

Explanation:

Let the speed of current = x km/h

Speed of boat = 9 km/h ( given )

Thus, the speed in upstream = (9 - x) km/h

Also, the speed in downstream = x km/h (because the boat is stationary in downstream)

Total distance = 6 km ( from N to the point he reached )

Since, Time = distance/ speed

According to the question,

`(6)/(9-x)+(6)/(x)=\text{ 2 hours 40 minutes}`

`(6)/(9-x)+(6)/(x)=2(40)/(60)`

`6[(1)/(9-x)+(1)/(x)]=2(2)/(3)`

`6[(1)/(9-x)+(1)/(x)]=(8)/(3)`

`(1)/(9-x)+(1)/(x)=(8)/(18)`

`(x+9-x)/(9x-x^2)=(4)/(9)`

`(9)/(9x-x^2)=(4)/(9)`

`81=36x-4x^2`

`4x^2-36x+81=0`

`4x^2-18x-18x+81=0`

`2x(2x-9)-9(2x-9)=0`

`(2x-9)(2x-9)=0`

`\implies 2x - 9 = 0\implies x = (9)/(2)=4.5`

Hence, the speed of current = x km/h = 4.5 km/h