Question

A player holds two baseballs a height h above the ground. He throws one ball vertically upward at speed v0 and the other vertically downward at the same speed. Obtain expressions for the speed of each ball as it hits the ground and the difference between their times of flight. (Assume the positive direction is upward.) HINT

Answer 1

a) v = √(v₀² + 2g h), b) Δt = 2 v₀ / g

Step-by-step explanation:

For this exercise we will use the mathematical expressions, where the directional towards at is considered positive.

The velocity of each ball is

ball 1. thrown upwards vo is positive

v² = v₀² - 2 g (y-y₀)

in this case the height y is zero and the height i = h

v = √(v₀² + 2g h)

ball 2 thrown down, in this case vo is negative

v = √(v₀² + 2g h)

The times to get to the ground

ball 1

v = v₀ - g t₁

t₁ =
`(v_(o) - v )/( g)`

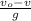
ball 2

v = -v₀ - g t₂

t₂ = - \frac{v_{o} + v }{ g}

From the previous part, we saw that the speeds of the two balls are the same when reaching the ground, so the time difference is

Δt = t₂ -t₁

Δt =
`(1)/(g) \ [(v_(o) - v) - ( - v_(o) - v) ]`

Δt = 2 v₀ / g