Question

Given a right triangle, what is a if ZB = 70° and b = 16? (Round youranswer to the nearest tenth.)

Answer 1

Considering the right triangle ABC

Side a is opposite to ∠A and adjacent to ∠B

Side b is opposite to ∠B and adjacent to ∠A

To determine the length of "a" given that we know the length of b and the measure of ∠B, you have to apply the trigonometric ratio of the tangent which is defined as follows:

`\tan \theta=(opposite)/(adjacent)`

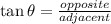
The tangent of an angle "θ" is equal to the quotient between the opposite side of the angle and the adjacent side.

As mentioned before, considering ∠B, side b is opposite to this angle, and side a is adjacent to it.

Replace ∠B=70º and b=16 into the expression of the tangent:

`\begin{gathered} \tan B=(b)/(a) \\ \tan 70=(16)/(a) \end{gathered}`

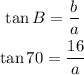
Multiply both sides by "a" to take the term from the denominator's place:

`\begin{gathered} a\tan 70=a\cdot(16)/(a) \\ a\tan 70=16 \end{gathered}`

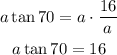
Divide both sides by the tangent of 70 to determine the length of a:

`\begin{gathered} (a\tan70)/(\tan70)=(16)/(\tan 70) \\ a=(16)/(\tan 70) \\ a=5.82\approx5.8 \end{gathered}`

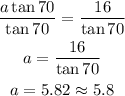
Side a is 5.8 units long. (first option)