Question

A Native American tepee is a conical tent. Find the number of skins needed to cover a teepee 10 ft. in diameter and 12 ft. high. Each skin covers 15 sq. ft. (use = 3.14)

Answer 1

Since it is conical, we need to find the surface area of the top of the conical shape.

If we unfold the top part of the cone, we will have a section of a circle:

The circunference of this section is the same as the total circunference of the base of the cone, which we can get from its radius (half its diamtere):

`C=2\pi r=2\pi\cdot(D)/(2)=2\pi\cdot(10)/(2)=10\pi`

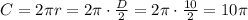
If we visualize the cone by the side, we see that it forms a isosceles triangle which the same height and the base euqal to the diameter:

So, we can calculate "R", the radius of the unfolded cone, using the Pythagora's Theorem:

`\begin{gathered} R^2=h^2+((D)/(2))^2 \\ R^2=12^2+5^2 \\ R^2=144+25 \\ R^2=169 \\ R=\sqrt[]{169} \\ R=13 \end{gathered}`

The circunference of a section of a circle is the circunferece of the total circle times the fraction of the section represents of the total circle. Let's call ths fraction "f", this means that:

`\begin{gathered} C_(total)=f\cdot C \\ C_(total)=2\pi R=2\pi\cdot13=26\pi \\ C=10\pi \\ f\cdot26\pi=10\pi \\ f=(10\pi)/(26\pi)=(5)/(13) \end{gathered}`

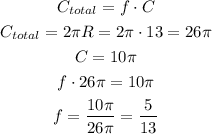
The area will follow the same, the area of the section is the fraction "f" times the total area of the circle, so:

`\begin{gathered} A_(total)=\pi R^2=\pi13^2=169\pi \\ A=f\cdot A_(total)=(5)/(13)\cdot169\pi=65\pi\approx65\cdot3.14=204.1 \end{gathered}`

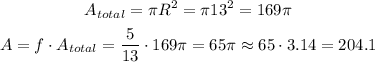
So, the surface area of the top of the cone is 204.1 ft². Since each skin covers 15 ft², we can calculate how many skins we need by dividing the total by the area of each skin:

`(204.1)/(15)=13.60666\ldots`

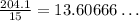
This means that we need 13.60666... skins, that is, 13 is not enough, we need one more, so we need a total of 14 skins.