Since it is conical, we need to find the surface area of the top of the conical shape.
If we unfold the top part of the cone, we will have a section of a circle:
The circunference of this section is the same as the total circunference of the base of the cone, which we can get from its radius (half its diamtere):
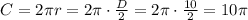
If we visualize the cone by the side, we see that it forms a isosceles triangle which the same height and the base euqal to the diameter:
So, we can calculate "R", the radius of the unfolded cone, using the Pythagora's Theorem:
![\begin{gathered} R^2=h^2+((D)/(2))^2 \\ R^2=12^2+5^2 \\ R^2=144+25 \\ R^2=169 \\ R=\sqrt[]{169} \\ R=13 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/er6vlx1alrsszs9toc1a.png)
The circunference of a section of a circle is the circunferece of the total circle times the fraction of the section represents of the total circle. Let's call ths fraction "f", this means that:
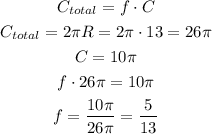
The area will follow the same, the area of the section is the fraction "f" times the total area of the circle, so:
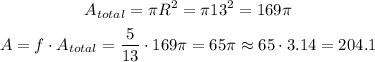
So, the surface area of the top of the cone is 204.1 ft². Since each skin covers 15 ft², we can calculate how many skins we need by dividing the total by the area of each skin:
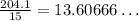
This means that we need 13.60666... skins, that is, 13 is not enough, we need one more, so we need a total of 14 skins.