Answer:
454 miles.
Explanation:
Refer the attached figure.
A cruise ship travels 310 miles due east i.e. AB = 310 miles
Now a cruise turns 20 degrees north of east .i.e.∠CBE = 20°
Using linear pair :Sum of angles = 180°
∠CBA+∠CBE=180°
∠CBA=180°-20° =160°
It travels 150 miles its new course i.e. BC= 150 miles.
Now we are supposed to find How far is the cruise ship from its initial position
Now using cosine rule:
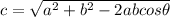
a =BC = 150 miles
b= Ab = 310 miles
c = AC
Substitute the values.
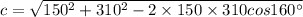
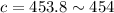
Thus the cruise ship is 454 miles from its initial position.