Question

These two functions represent the growth of two different bacterial cultures in terms of the number of bacteria after x days.

f(x) = 2,000(2)^x (other one on the graph)

Answer the following:
A) Which function has the higher initial amount of bacteria? g(x) or f(x)
B) Which function has the greater amount of bacteria after two days? g(x) or f(x)

Answer 1

A. The function f(x) has the higher initial amount of bacteria.

B. The function g(x) has the higher amount of bacteria after two days.

Explanation:

The given function is

`f(x)=2000(2)^x`

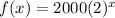
The graph of g(x) passing through the points (0,1000) and (1,3000). So the initial value is 1000 and the growth factor is 3.

The function g(x) is

`g(x)=1000(3)^x`

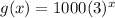
Part A:

Substitute x=0, to find the initial blue of the functions.

`f(0)=2000(2)^0=2000`

`g(0)=1000(3)^0=1000`

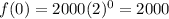
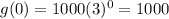
Since 2000>1000, therefore the function f(x) has the higher initial amount of bacteria.

Part B:

Substitute x=2, to find the amount of bacteria after two days.

`f(2)=2000(2)^2=8000`

`g(2)=1000(3)^2=9000`

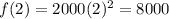
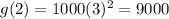
Since 8000<9000, therefore the function g(x) has the higher amount of bacteria after two days.