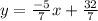Question

(-2,6),(5,1) write an equation for the line in point slope form .Then rewrite the equation in slope intercept form

Answer 1

The point-slope equation is the following:

`y-y_1=m(x-x_1)`

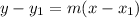
Where (x1, y1) is a point of the line and m is the slope.

The slope is calculated as:

`m=(y_2-y_1)/(x_2-x_1)`

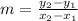
Where (x1, y1) and (x2, y2) are points of the line. So, replacing (x1, y1) by (-2, 6) and (x2, y2) by (5, 1), we get:

`m=(1-6)/(5-(-2))=(-5)/(5+2)=(-5)/(7)`

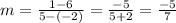
Then, the point-slope form is:

`\begin{gathered} y-6=(-5)/(7)(x-(-2)) \\ y-6=(-5)/(7)(x+2) \end{gathered}`

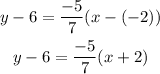
Finally, to rewrite the equation in slope-intercept form, we need to solve for y as:

`\begin{gathered} y-6=(-5)/(7)(x+2) \\ y-6=(-5)/(7)x+(-5\cdot2)/(7) \\ y-6=(-5x)/(7)-(10)/(7) \\ y=(-5x)/(7)-(10)/(7)+6 \\ y=(-5x)/(7)+(32)/(7) \end{gathered}`

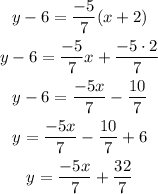
Answer: Point-slope form:

`y-6=(-5)/(7)(x+2)`

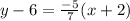
Slope-Intercept form:

`y=(-5)/(7)x+(32)/(7)`