Question

the jet stream is a wind current that flows across the US from west to east. Flying with the jet stream, an airplane flew 2700 miles in 4.5 hours. Against the same wind, the return trip took 6 hours. Find the speed of the plane in stil air and the speed of the jet stream.

Answer 1

The speed of the plane in still air and the speed of the jet stream are 525 miles per hour and 75 miles per hour.

Explanation:

From Mechanical Physics, we know that absolute velocity of the airplane (
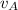`v_(A)`) is equal to sum of the absolute velocity of the jet steam
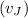`(v_(J))` and the relative velocity of the airplane with respect to jet stream (velocity of the airplane in still air) (
`v_(A/J)`). Al velocities are measured in miles per hour. Let suppose that both jet stream and airplanes travels at constant velocity. Now, we construct the following system of linear equations:

Flight with the jet stream

`v_(J)+v_(A/J) = (2700\,mi)/(4.5\,h)`

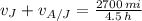
`v_(J)+v_(A/J) = 600\,(mi)/(h)` (1)

Flight against the jet stream

`v_(J) -v_(A/J) = -(2700\,mi)/(6\,h)`

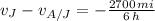
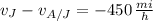`v_(J)-v_(A/J) = -450\,(mi)/(h)` (2)

The solution of this system of linear equations is:

`v_(J) = 75\,(mi)/(h)`,
`v_(A/J) = 525\,(mi)/(h)`

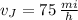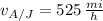
The speed of the plane in still air and the speed of the jet stream are 525 miles per hour and 75 miles per hour.