Question

Please solve this 4 the grade algebra problem? A group of students calculated their average score at a spelling bee. They realized that if one of them scored 9 more points , their average score will be 81 points. if one of them scored 3 points less, their average score will be 78 points. How many students were in the group?

Answer 1

let x = original average score
let y = be the number of students

We need to write two equation using the information given in the scenario in order to work them simultaneously and obtain the results.

let
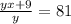
`(yx + 9)/(y) = 81` .... (1)
so x is the original average, so we multiply that average by the amount of students [y × x] in order to obtain their cumulative score then you add the nine to that score (because a student got 9 more points) [yx + 9]. Then you divide that sum by the amount of student in order to get the new average which the question says would be 81


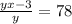
`(yx - 3)/(y) = 78` ...... (2)
so x is the original average, so we multiply that average by the amount of students [y × x] in order to obtain their cumulative score then you subtract three from that score since one student got three less points [yx - 3]. Then you divide by the number of students (y) and you should 78 like the question says.


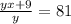`(yx + 9)/(y) = 81` .... (1)

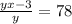`(yx - 3)/(y) = 78` ...... (2)

Now simplify each equation by separating the LHS

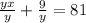`(yx)/(y) + (9)/(y) = 81`..... (1a)

`(yx)/(y) - (3)/(y) = 78`...... (2a)

By subtracting eq (2a) from eq (1a) in order to eliminate x

`(yx)/(y) - (yx)/(y) + (9)/(y) - (- (3)/(y)) = 81 - 78`


`(12)/(y) = 3`


`(12)/(3) = y`

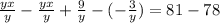
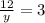
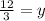⇒ y = 4

Since y = the number of students
then the number of students = 4