Question

A car pulls on to an onramp with an initial speed of 23.8 mph. The length of the onramp is 852 ft and the car needs to be moving at 45.7 mph at the end of the ramp to merge with traffic. What constant rate of acceleration (in ft/sec2) is required in order to accomplish this

Answer 1

The constant rate of acceleration required in order to accomplish this is 1.921 feet per square second.

Step-by-step explanation:

Let suppose that car accelerates uniformly in a rectilinear motion. Given that initial and final speeds and travelled distances are known, then the acceleration needed by the vehicle (
`a`), measured in feet per square second, is determined by the following kinematic formula:

`a = (v_(f)^(2)-v_(o)^(2))/(2\cdot \Delta x )` (1)

Where:

`v_(o)`,
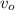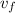`v_(f)` - Initial and final speeds, measured in feet per second.

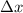`\Delta x` - Travelled distance, measured in feet.

If we know that
`v_(o) = 34.907\,(ft)/(s)`,
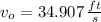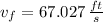`v_(f) = 67.027\,(ft)/(s)` and
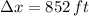`\Delta x = 852\,ft`, then acceleration needed to accomplish the task is:

`a = 1.921\,(ft)/(s^(2))`

The constant rate of acceleration required in order to accomplish this is 1.921 feet per square second.