Question

A rectangular box is to have a square base and a volume of 40 ft3. If the material for the base costs $0.37 per square foot, the material for the sides costs $0.05 per square foot, and the material for the top costs $0.13 per square foot, determine the dimensions of the box that can be constructed at minimum cost.

length
heigth
width

Answer 1

so hmm if you check the picture below, the area of the base is x*x and the top's is x*x and the sides, are 4 rectangles, each with area of h*x

thus
`\bf \textit{volume of a rectangular prism}\\\\ V=lwh\qquad \begin{cases} l=length\\ w=width\\ h=height\\ ----------\\ l=w=x\\ base=l\cdot w\\ \qquad x\cdot x\implies x^2\\ V=40 \end{cases}\implies \begin{array}{llll} 40=x^2h\\\\ \cfrac{40}{x^2}=\boxed{h} \end{array}\\\\ -----------------------------`


`\bf \begin{array}{llll} \textit{area of the base}\\\\ A_b=x^2 \end{array} \qquad \begin{array}{llll} \textit{area of the top}\\\\ A_b=x^2 \end{array} \\\\\\ \textit{area of the sides, or lateral area}\\\\ A_l=xh+xh+xh+xh\implies 4xh\implies 4x\cdot \boxed{\cfrac{40}{x^2}}\implies \cfrac{160}{x}`

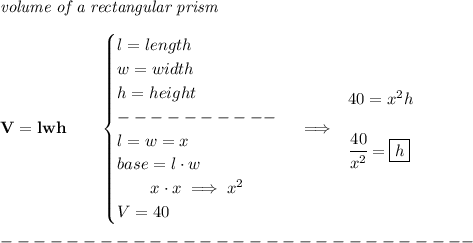
now, the cost function, or C(x), well, we know how much area is going to be used in x-term, so let's just apply the cost to each


`\bf C(x)=0.37A_b+0.13A_t+0.05A_s\to C(x)=0.37x^2+0.13x^2+\cfrac{8}{x} \\\\\\ C(x)=0.5x^2+8x^(-1)`

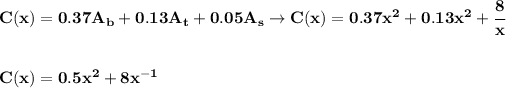
so.... now just get the derivative of C(x) and zero it out out and check the critcal points for any minima