Question

For the circle, a 70° central angle cuts off an arc of 8 inches what is the circumference of the circle (there are 360° in a circle)

Answer 1

there are 360° in a circle, now, this "sector" of the circle has an angle of 70°, so for 70°, there are 8in or circumference, or arc length

how much arc length or circumference in 360° then?

well
`\bf \begin{array}{ccllll} degrees&circumference\\ -----&--------\\ 70&8\\ 360&x \end{array}\implies \cfrac{70}{360}=\cfrac{8}{x}`

solve for "x"

Answer 2

Answer: 41.14 inches

Explanation:

The formula to find the length of an arc :-

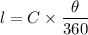`l=C*(\theta)/(360)`, where C is the circumference of the circle,
`\theta` is the central angle cuts off an arc of length 'l'.

Given : Central angle : =
`\theta = 70{\circ}`

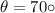
Length of arc:
`l= 8\ inches`

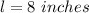
Now, substitute all theses value in the above formula , we get

`8=C*(70)/(360)\\\\\Rightarrow\ 8=C*(7)/(36)\\\\\Rightarrow\ C=(36*8)/(7)=41.1428571429\approx41.14\text{ inches}`

Hence, the circumference of the circle is about 41.14 inches.