Question

Graph of a parabola opening down at the vertex 0 comma 36 crossing the x–axis at negative 6 comma 0 and 6 comma 0. Courtesy of Texas Instruments In the distance, an airplane is taking off. As it ascends during take-off, it makes a slanted line that cuts through the rainbow at two points. Create a table of at least four values for the function that includes two points of intersection between the airplane and the rainbow. Analyze the two functions. Answer the following reflection questions in complete sentences. What is the domain and range of the rainbow? Explain what the domain and range represent. Do all of the values make sense in this situation? Why or why not? What are the x- and y-intercepts of the rainbow? Explain what each intercept represents. Is the linear function you created with your table positive or negative? Explain. What are the solutions or solution to the system of equations created? Explain what it or they represent

Answer 1

Thats a lot could you maybe seperate the questions?

Answer 2

All in the Explanation

Explanation:

Vertex of the Parabola=(0,36)

X-Intercepts are (-6,0) and (0,6)

An equation with roots 6 and -6 is determined below;

x=6 or x=-6

(x-6)(x+6)=0

`x^2-36=0\\f(x)=-x^2+36`

`\left|\begin{array}c---&---\\x & f(x)\\---&---\\-6&0\\-3&27\\0&36\\3&27\\6&0\end{array}\right|`

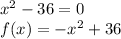
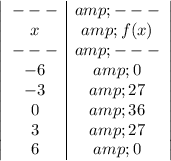
The two points of the slanted line cutting through the parabola are (-6,0) and (3,27).

First, we determine the equation of the line.

• Gradient of points (-6,0) and (3,27).

The slope of a line passing through the two points and is given by
`\displaystyle{\large{{m}=\frac{{{y}_{{2}}-{y}_{{1}}}}{{{x}_{{2}}-{x}_{{1}}}}}}.`

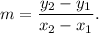
We have that
`x_1=-6, y_1=0, x_2=3, y_2=27.`

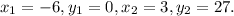
Plug the given values into the formula for slope:
`m=(\left(27\right)-\left(0\right))/(\left(3\right)-\left(-6\right))=(27)/(9)=3.`

Now, the y-intercept is
`\displaystyle{\large{{c}={y}_{{1}}-{m}\cdot{x}_{{1}}}} (or\: \displaystyle{\large{{c}={y}_{{2}}-{m}\cdot{x}_{{2}}}})` the result is the same).

`c=0-\left(3\right) \cdot \left(-6\right)=18.`

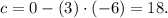
Finally, the equation of the line can be written in the form
`\displaystyle{\large{{y}={m}{x}+{c}}}.`

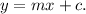
f(x)=3x+18.

• The domain of the rainbow is the set of values of x while the range is the set of values of f(x).
• The x- and y-intercepts of the rainbow are the points where the curve cuts the x and y axis respectively.

1. The x-intercepts are (-6,0) and (6,0)
2. The y-intercept is (0,36)

The linear function y=3x+18 is positive since its slope, m is positive.

The system of equation created by the parabola and the curve is determined below:

`f(x)=-x^2+36\\f(x)=3x+18\\3x+18=-x^2+36\\-x^2+36-3x-18=0\\-x^2-3x+18=0`

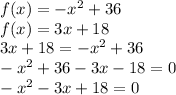
The solution of the system
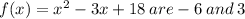`f(x)=x^2-3x+18 \: are -6\:and \:3`. They represent the point of intersections of the curve and parabola.