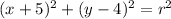Answer:
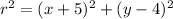
Explanation:
we know that
The equation of the circle into center-radius form is equal to
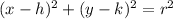
where
(h,k) is the center of the circle
r is the radius of the circle
Step 1
we have
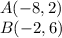
Find the center of the circle
The center of the circle is the midpoint between point A and point B
The formula to calculate the midpoint is equal to
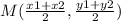
substitute the values
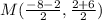
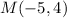
the equation of the circle is equal to