Question

(a) Find a function that models the population (b) Use the function from part (a) to estimate the fox population in the year 2008.

Answer 1

Given:

• Growth rate = 4% per year ==> 0.04

,

• Initial population in year 2000 = 23000

Let's solve for the follosing:

• (a). Find a function that models the population

To find a function that models the population, apply the exponential growth formula:

`f(x)=a(1+r)^x`

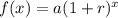
Where:

a is the initial value

r is the growth rate in decimal.

Thus, we have the function:

`\begin{gathered} P(t)=23000(1+0.04)^t \\ \\ P(t)=23000(1.04)^t \end{gathered}`

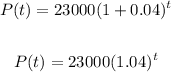
In the function above, t is the number of years after year 2000.

• (b). Use the function from part (a) to estimate the fox population in the year 2008.

Number of years from 2000 to 2008 ==> 2008 - 2000 = 8 years

Hence, to find the population in the year 2008, substitute 8 for t in the function from part(a) and solve.

We have:

`\begin{gathered} P(8)=23000(1.04)^8 \\ \\ P(8)=23000(1.36856905) \\ \\ P(8)=31477.1\approx31477 \end{gathered}`

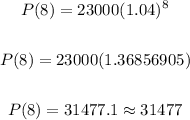
Therefore, the estimated population in the year 2008 will be 31477.

ANSWER:

• (a). P(t) = 23000(1.04)ᵗ

• (b). 31477