Given:
• Growth rate = 4% per year ==> 0.04
,
• Initial population in year 2000 = 23000
Let's solve for the follosing:
• (a). Find a function that models the population
To find a function that models the population, apply the exponential growth formula:
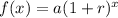
Where:
a is the initial value
r is the growth rate in decimal.
Thus, we have the function:
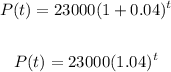
In the function above, t is the number of years after year 2000.
• (b). Use the function from part (a) to estimate the fox population in the year 2008.
Number of years from 2000 to 2008 ==> 2008 - 2000 = 8 years
Hence, to find the population in the year 2008, substitute 8 for t in the function from part(a) and solve.
We have:
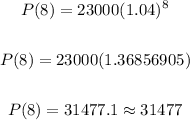
Therefore, the estimated population in the year 2008 will be 31477.
ANSWER:
• (a). P(t) = 23000(1.04)ᵗ
• (b). 31477