Question

A homeowner purchased 920 feet of fencing to create an enclosed play space for the family dog. One side of the play space is against the house and will not require fencing. The other three sides will be fenced. Let represent the width of the fence that is perpendicular to the house and let represent the length of the fence that is parallel to the house. (Round your answers to the nearest hundredth. Show all work.)House 1) Write an equation to represent the available fence and the sides.2) Write an equation/formula to represent the length of the play space, in terms of .3) Write a formula for the area of the play space in function notation, (). (Hint: Area = length * width)4) What is the maximum area? Show all work.5) Find are the dimensions needed to create the maximum area

Answer 1

Let:

x = Width of the fence that is perpendicular to the house

y = Width of the fence that is parallel to the house

1) Since y is parallel to the house, the width x needs to be counted twice and the width y only counts once. The total length of the perimeter is:

P = 2x + y

The perimeter is known to be 920 feet of fencing, thus:

2x + y = 920

2) From the equation above, we can solve for y as follows:

y = 920 - 2x

3) The area of a rectangle is the product of both dimensions:

`A=x\cdot y`

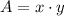
Substituting the expression for y:

`\begin{gathered} A=x(920-2x) \\ A=920x-2x^2 \end{gathered}`

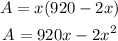
To give the result of part 4, I need to solve part 5 first.

5) To create the maximum area, we take the first derivative and equate it to 0:

`A^(\prime)=920-4x=0`

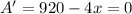
Solving the equation:

x = 920/4

x = 230

The value of y is:

y = 920 - 2x

y = 920 - 460

y = 460

The dimensions are x = 230 feet and y = 460 feet

4)

Substituting into the formula of the area:

`\begin{gathered} A=920\cdot230-2\cdot230^2 \\ \text{Operating:} \\ A=105,800 \end{gathered}`

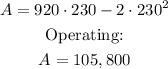
The maximum area is 105,800 square feet