Question

Assume the pattern continues for the following sequence of tile figures; that is, each tile divided into four tiles in the subsequent figure. Let S(n) be the function giving the total number of tiles in the nth figure. Find a formula for S(n) in terms of n.

Answer 1

The sequence given can be seen as:

1, 4, 16, .......

From this three terms we notice that the terms of this sequence are obtain by multiplying the previous term by 4, this means that this a geometric sequence.

We know that a geometric series is given by:

`a_n=ar^(n-1)`

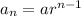
where a is the first term and r is the common ratio. In this case the common ratio is 4, then the sequence is:

`a_n=4^(n-1)`

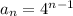
This gives the total number of tiles in the nth figure, then we can rewrite as:

`S(n)=4^(n-1)`