Question

The motion of a piston of a car engine approximates simple harmonic motion. Given that the stroke (twice the amplitude) is 0.100 m, the engine runs at 2,800 r/min, and the piston starts at the middle of its stroke, find the equation for the displacement d as a function of t. Sketch two cycles.

Answer 1

y = - 0.050 sin (131.59t )

Step-by-step explanation:

In this exercise we are told to approximate the movement of a piston to the simple harmonic movement

y = A cos (wt + Ф)

in this case they indicate that the stroke (C) of the piston is twice the amplitude

C = 2A

A = C / 2

angular velocity is related to frequency

w = 2π f

let's substitute

y =
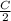`(C)/(2)` cos (2π f t +Ф)

To find the phase (fi) we will use the initial conditions, the piston starts at the midpoint of the stroke, if we create a reference system where the origin is at this point

y = 0 for t = 0

we substitute in the equation

0 = \frac{C}{2} cos (0 + Ф)

The we sew zero values ​​for the angles of Ф = π/2 rad

we substitute in the initial equation

y = \frac{C}{2} cos (2π f t + π/2)

let's use the double angle relationship

cos ( a +90) = cos a cos 90 - sin a sin 90

cos (a+90) = - sin a

y = -\frac{C}{2} sin (2πf t )

let's reduce the frequency to SI units

f = 200 rpm (2π rad / 1rev) (1 min / 60s) = 20.94 rad / s

we substitute the given values

y = -
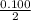`(0.100)/(2)` sin (2π 20.94 t )

y = - 0.050 sin (131.59t )