Given: The graph of the circle shown in the image
To Determine: The equation of the given circle
Solution
The general equation of a circle given the center and the radius is as shown below
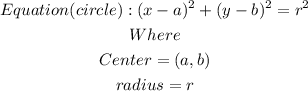
Let us determine the center and radius of the given circle as shown below
It can be observed that
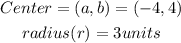
Let us substitute the center and the radius into the equation

Hence, the equation of the circle is
(x + 4)² + (y - 4)² = 9