Question

Instructions: Given the graph of the circle, find the equation

Answer 1

Given: The graph of the circle shown in the image

To Determine: The equation of the given circle

Solution

The general equation of a circle given the center and the radius is as shown below

`\begin{gathered} Equation(circle):(x-a)^2+(y-b)^2=r^2 \\ Where \\ Center=(a,b) \\ radius=r \end{gathered}`

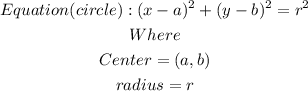
Let us determine the center and radius of the given circle as shown below

It can be observed that

`\begin{gathered} Center=(a,b)=(-4,4) \\ radius(r)=3units \end{gathered}`

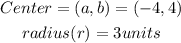
Let us substitute the center and the radius into the equation

`\begin{gathered} Equation(circle):(x-a)^2+(y-b)^2=r^2 \\ a=-4 \\ b=4 \\ r=3 \\ Equation(circle)=(x+4)^2+(y-4)^2=3^2 \\ =(x+4)^2+(y-4)^2=9 \end{gathered}`

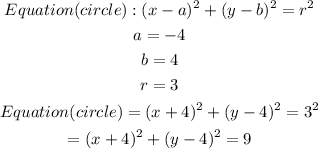
Hence, the equation of the circle is

(x + 4)² + (y - 4)² = 9