Question

Bob wants to create two pens, as shown in the figure. One pen is for a garden and it needs a heavy duty fence to keep out the critters. This heavy duty fence costs $15 per foot. The dog pen shares a side with the garden and has a lighter weight fence on the other three sides that costs $5 per foot. If each pen is to have an area of 2,744, find the values of x and y that would minimize the total cost of the fencing.

Answer 1

`\bf \textit{the area of either pen is 2744, thus}\\\\ A=xy\implies 2744=xy\implies \cfrac{2744}{x}=y`


`\bf \begin{array}{llll} \textit{perimeter of the garden pen}\\\\ P=2(x+y)\\\\ P=2\left( x+ \cfrac{2744}{x}\right)\\\\ P=2x+\cfrac{5488}{x}\\ ----------\\ \textit{cost of it}\\\\ C=15\left( 2x+\cfrac{5488}{x} \right)\\\\ C=30x+\cfrac{82320}{x} \end{array}\qquad \begin{array}{llll} \textit{perimeter of the dog pen}\\\\ P=2x+y\\\\ P=2x+\cfrac{2744}{x}\\ ----------\\ \textit{cost of it}\\\\ C=5\left( 2x+\cfrac{2744}{x} \right)\\\\ C=10x+\cfrac{27440}{x} \end{array}`

notice... the dog's pen perimeter, does not include the side that's bordering the garden's, since that side will use the heavy duty fence, instead of the light one

so, the sum of both of those costs, will be the C(x)


`\bf C(x)=\left( 30x+\cfrac{82320}{x} \right)+\left( 10x+\cfrac{27440}{x} \right) \\\\\\ C(x)=40x+\cfrac{109760}{x}`

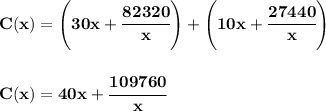
so, just take the derivative of it, and set it to 0 to find the extremas, and do a first-derivative test for any minimum