Question

Carmelo is selling his hockey and baseball card collection. Hockey cards, x, sell for $0.03 and baseball cards, y, sell for $0.05. The number of hockey cards Carmelo sells is at least six times the number of baseball cards he sells. He has at most 525 cards to sell.

What is the maximum revenue he can make?

Answer 1

x= 6y

x + y = 525

solving these two equations

6y+y = 525
y = 75

x = 6*75=450

Total revenue = 450 * .03+ 75 * .05
= 17.25

Answer 2

Let x be the number of hockey cards, x≥0 (this inequality is represented in attached diagram by red color) and y be the nubmer of baseball cards, y≥0 (this inequality is represented in attached diagram by blue color).

If the number of hockey cards Carmelo sells is at least six times the number of baseball cards he sells, then x≥6y (this inequality is represented in attached diagram by green color).

If he has at most 525 cards to sell, then x+y≥525 (this inequality is represented in attached diagram by violet color).

These for inequalities together form the triangle (see diagram). This triangle has vertices at points (0,0), (450,75) and (525,0).

He sells hockey cards for $0.03 and baseball cards for $0.05, then the function of revenue he can make is

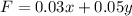`F=0.03x+0.05y` (black line).

Translating this line up and down you can see how the value of F changes. It is known that maximum value of F will be at triangle's vertices (limit points of the area).

Find value of this function in triangle's vertices:

• 
  `F(0,0)=0.03\cdot 0+0.05\cdot 0=0;`
• 
  `F(450,75)=0.03\cdot 450+0.05\cdot 75=17.25;`
• 
  `F(525,0)=0.03\cdot 525+0.05\cdot 0=15.75.`

Answer: the maximum revenue he can make is $17.25.