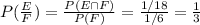Answer: 1/3
Explanation:
Since, when the two dice are rolled,
The total outcomes, n(S) = 6 × 6 = 36,
Now, the possible outcomes that the sum of the two rolls is less than 9 when two dice are rolled
E = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (4,1), (4,2), (4,3), (4,4), (5,1), (5,2), (5,3), (6,1), (6,2)}
Now, The possible outcomes that the first roll is a 6,
F = { (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}
n(F) = 6,
⇒
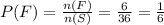
Since, E ∩ F = { (6,1), (6,2) }
⇒ n( E ∩ F ) = 2
Thus,
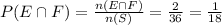
Hence, the probability that the sum of the two rolls is less than 9, given that the first roll is a 6