Answer:
0,1, 2 and 3 employees judging their co-workers by cleanliness would be considered unusual.
Explanation:
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
Can be approximated to a normal distribution, using the expected value and the standard deviation.
The expected value of the binomial distribution is:
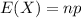
The standard deviation of the binomial distribution is:

An outcome is considered unusual if it is more than 2.5 standard deviations from the mean.
Eighty-two percent of employees make judgements about their co-workers based on the cleanliness of their desk.
This means that
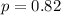
You randomly select 7 employees and ask them if they judge co-workers based on this criterion.
This means that
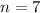
Mean:
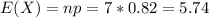
Standard deviation:
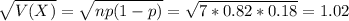
Two and a half standard deviations above the mean:
Will be higher than 7, so no possible values.
Two and a half standard deviations below the mean:
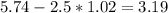
So 0,1, 2 and 3 employees judging their co-workers by cleanliness would be considered unusual.