Question

A particular population of birds are black, blue and red. An investigator believes that 20% are black, 30% are blue, and 50% are red. To test her hypothesis, the investigator captures 100 birds and records their color, then releases the birds back into the wild. In the sample of 100 birds, she observes 25 are black, 35 are blue and 40 are red. Calculate the Chi-Square Statistic.

Answer 1

0.0291

Explanation:

To Calculate the Chi-Square Statistic, we use the approach:

1. The expected value would be subtracted from the observed value
`(O-E)`

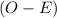
2. Next, Square the difference

3. Divide the squares by the expected value
`(O-E)^(2)/E`and

4. Finally, sum all the values for
`(O-E)^(2)/E`

Solution:

Black:

Observed value: 25% or 0.25

Expected value: 20% or 0.2

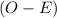`(O-E)` = 0.25-0.2 =

`(O-E)^(2)` =
`0.05^(2)` = 0.0025

`(O-E)^(2)/E` = 0.0025/0.2 = 0.0125

Blue:

Observed value: 35% or 0.35

Expected value: 30% or 0.3

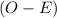`(O-E)` = 0.35-0.3 = 0.05

`(O-E)^(2)` =
`0.05^(2)` = 0.0025

`(O-E)^(2)/E` = 0.0025/0.3 = 0.0083

Red:

Observed value: 40% or 0.4

Expected value: 50% or 0.5

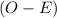`(O-E)` = 0.4-0.5 = 0.1

`(O-E)^(2)` =
`0.1^(2)` = 0.01

`(O-E)^(2)/E` = 0.01/0.5 = 0.02

Total
`(O-E)^(2)/E` = 0.0125+0.0083+0.0083 = 0.0291.

Therefore, Chi-Square Statistic
`x^(2)` = 0.0291