Question

A lumber company is making doors that are 2058.0 millimeters tall. If the doors are too long they must be trimmed, and if the doors are too short they cannot be used. A sample of 15 is made, and it is found that they have a mean of 2044.0 millimeters with a standard deviation of 17.0. A level of significance of 0.05 will be used to determine if the doors are either too long or too short. Assume the population distribution is approximately normal. Find the value of the test statistic. Round your answer to three decimal places.

Answer 1

Answer: 3.190

Explanation:

If the population distribution is normal, and population standard deviation is unknown, then

The test statistic is given by :-

`t=\frac{\overline{x}-\mu}{(s)/(√(n))}`

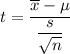
, where
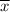`\overline{x}` = sample mean ,
`\mu` = population mean , n= sample size, s= sample standard deviation.

Given:
`\mu` = 2058

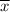`\overline{x}` = 2044

s= 17

n= 15

Test statistic:

`t= (2044-2058)/((17)/(√(15)))\approx3.190`

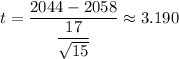
Hence, the value of the test statistic is 3.190 [Rounded to the three decimal places.]