Question

Identify a sequence of transformations that maps triangle ABC onto triangle A"B"C" in the image below.

A. clockwise 270° rotation; reflection over x-axis
B. counterclockwise 90° rotation; reduction
C. counterclockwise 270° rotation; reflection over the y-axis
D. enlargement; clockwise 90° rotation


Could someone explain this to me?

Answer 1

The A"B"C" is the red triangle. What happened is it was a 90 degree rotation around the 0, then an enlargement. The correct answer is D.

Hope I helped.

Answer 2

The correct option is B.

Explanation:

It is given that triangle A"B"C" is the image of triangle ABC after transformation.

From the given figure it is noticed that the point C lies on positive y-axis and point C" lies on negative x-axis.

It means the figure is rotated either counterclockwise 90° or clockwise 270°. The rotation rule is

`(x,y)\rightarrow (-y,x)`

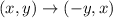
The corresponding sides of image A"B"C" are smaller than the preimage ABC.

`k=(A`

Since k<0, therefore the transformation shows the reduction. The dilation rule is

`(x,y)\rightarrow (-(1)/(2)y,(1)/(2)x)`

`A(-3,0)\rightarrow (-(1)/(2)(0),(1)/(2)(-3))\rightarrow (0,-1.5)`

`B(3,0)\rightarrow (-(1)/(2)(0),(1)/(2)(3))\rightarrow (0,1.5)`

`C(0,5.2)\rightarrow (-(1)/(2)(5.2),(1)/(2)(0))\rightarrow (-2.6,0)`

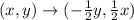
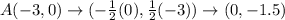
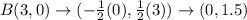
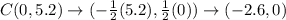
Option B is correct.