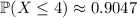Let
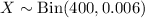
be the random variable representing the number of genes that do get mutated. Here
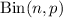
denotes a binomial distribution with parameters

(total number of genes) and
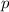
(probability of mutation).
Then the probability that *at most* 4 genes get mutated is
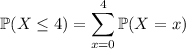
where
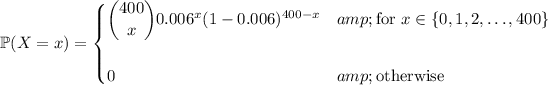
You should find that