Question

The gasoline prices in seven states are $1.96, $2.09, $1.79, $1.61, $1.75, $2.11, and $1.84. The median gasoline price is . The difference of the first and third quartiles in this set of gas prices is . NextReset

Answer 1

The median gasoline price is $1.84.

The difference of the first and third quartiles in this set of gas prices is 0.34

Explanation:

The median is a central position statistic that splits the distribution in two, that is, it leaves the same number of values ​​on one side as on the other.

The median of a set of numbers is the middle number in the set (after the numbers have been arranged from least to greatest) or, if there is an even number of data, the median is the average of the two middle numbers.

So, to find the median in the first place it is convenient to order the numbers from least to greatest:

1.61 ; 1.75 ; 1.79 ; 1.84 ; 1.96 ; 2.09 ; 2.11

Being 7 prices and being an odd number, the median is the value that occupies the central place of all the data. Then, the median gasoline price is 1.84.

Quartiles are values ​​that divide a data sample into four equal parts. That is, the quartiles are the three elements of an ordered data set that divide the set into four equal parts.

The first and third quartiles are calculated as:

given n ordered data, then

First quartile:
`(n+1)/(4)`

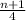
Third quartile:
`(3*(n+1))/(4)`

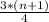
In this case:

First quartile:
`(7+1)/(4)=(8)/(4)=2`

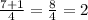
Third quartile:
`(3*(7+1))/(4)=(3*8)/(4) =(24)/(4)=6`

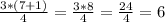
This means that the first quartile is in position 2 and the third quartile in position 6. So the value of the first quartile is 1.75 and the value of the third quartile is 2.09

The difference is the result of subtracting one number from another. In this case: 2.09 - 1.75= 0.34

The difference of the first and third quartiles in this set of gas prices is 0.34