Question

HELP!!!!!!!!!!!

The figure is made up of a hemisphere and a cylinder.

What is the exact volume of the figure?



Enter your answer in the box.

cm3

Answer 1

890 cubic cm is the exact volume of the figure

Explanation:

Volume of the hemisphere(V) is given by:

`V = (2)/(3) \pi r^3`

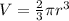
Volume of the cylinder(V') is given by:

`V' = \pi r^2h`

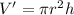
where, r is the radius and h is the height

As per the statement:

The figure is made up of a hemisphere and a cylinder.

In hemisphere:

radius(r) = 5 cm

then;

`V = (2)/(3) \pi 5^3 =(2)/(3) \pi \cdot 125`

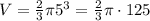
Use
`\pi = 3.14`

`V = (2)/(3) \cdot 3.14 \cdot 125 \approx 261.7 cm^3`

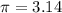
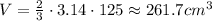
In Cylinder:

radius(r) = 5 cm and height(h) = 8 cm

then;

`V' = \pi 5^2 \cdot 8`

⇒
`V' = 3.14 \cdot 25 \cdot 8 = 628 cm^3`

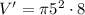
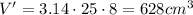
We have to find the exact volume of the figure

Total volume of the figure = V+V'

= 261.7+628 = 889.7 cubic cm

Therefore, 890 cubic cm is the exact volume of the figure

Answer 2

V=hpr^2+((4pr^3)/3)/2

V=3hpr^2+4pr^3/6

V=(18hpr^2+4pr^3)/6 and since h=8 and r=5

V=(3600p+500p)/6

V=4100p/6

V=2050p/3 cm^3