Question

The amount of time it takes a swimmer to finish the race is inversely proportional to the average speed of the swimmer. The swimmer finishes a race in 300 seconds with an average speed of 4 feet per second. Find the average speed of a swimmer if it takes 400 seconds to finish the race?

Answer 1

From the problem, the time is inversely proportional to the speed of the swimmer.

We can express this as :

`t=k((1)/(s))`

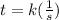
where t = time

s = speed

and

k is some constant.

The swimmer finishes a race in 300 seconds with an average speed of 4 ft/sec.

So t = 300 and s = 4

Using the proportion above, solve for the value of k :

`\begin{gathered} 300=k((1)/(4)) \\ k=4*300 \\ k=1200 \end{gathered}`

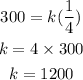
Now we have the value of k, the equation will be :

`t=1200((1)/(s))`

Find the speed when t = 400 secs.

Substitute t = 400, the speed will be :

`\begin{gathered} 400=1200((1)/(s)) \\ 400s=1200 \\ s=(1200)/(400)=3 \end{gathered}`

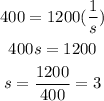
The answer is 3 feet per second