Question

According to the Fundamental Theorem of Algebra, the graph of f(x) = x^2 - 4x + 3, ____ has roots. From the graph we can see that it has _______ zeros.

Answer 1

According to the Fundamental Theorem of Algebra, the graph of f(x) = x^2 - 4x + 3, has 2 roots. From the graph we can see that it has two real zeros

Explanation:

Part 1)

we have

`f(x)=x^(2) -4x+3`

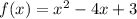
Is a polynomial of degree 2

According to the Fundamental Theorem of Algebra, any polynomial of degree n has n roots

so

The polynomial has 2 roots.

Part 2)

we know that

A "root" (or "zero") is where the polynomial is equal to zero

From the graph we can see that the polynomial is zero at x=-3 and x=-1

therefore

The function has two real zeros