Question

Frank stands 450 feet from the base of the Statue of Liberty. If the Statue of Liberty is 306 feet tall, what is the angle of depression from the top of the statue’s torch to Frank? Round the answer to the nearest tenth.

Answer 1

Let the angle of elevation be θ.


We have a right angled triangle with an opposite of 300.5 ft. (306 - 5.5) and an adjacent of 400 ft. Recalling SOH CAH TOA, tanθ = O/A.
tan(θ) = 300.5/400.
θ = tan^-1(300.5/400).
θ = 36.9°.

Answer 2

Answer: Angle of depression = 33.7°

Explanation:

Since we have given that

Length of base of the right angle triangle = 450 feet

Length of Frank = 5.5 feet

Length of Statue of Liberty = 306 feet

So, Length of perpendicular = 306-5.5=300.5 feet

So, in triangle , we will apply tangent of triangle:

`\tan \theta=(Perpendicular)/(Base)\\\\\tan \theta=(300.5)/(450)\\\\\tan \theta=0.6677\\\\\theta=\tan^(-1)(0.6677)\\\\\theta=33.7^\circ`

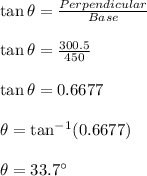
Hence, Angle of elevation = 33.7° = Angle of depression (By alternate interior angle).