Question

What are the roots of the polynomial equation x^3-5x+5=2x^2-5? Use a graphing calculator and a system of equations. Round noninteger roots to the nearest hundredth.

a. –3, –5
b. –2.24, –2, 2.24
c. –2.24, 2, 2.24
d. 3, 5

Answer 1

x^3-5x+5=2x^2-5

x^3-2x^2-5x+10=0 rearranging like so:

x^3-5x-2x^2+10=0 and factoring 1st and 2nd pair...

x(x^2-5)-2(x^2-5)

(x-2)(x^2-5) now you can factor the term in the second parentheses...

(x-2)(x+
`√(5)`)(x-
`√(5)`)

So the roots are -2.24, 2, 2.24

Answer 2

The right answer is c. –2.24, 2, 2.24

This question needs to be solved in two ways. First, using a graphing calculator. Next, using a system of equations.

1. Using a graphing calculator.

We have the following polynomial equation:

`x^3-5x+5=2x^2-5`

By ordering this equation we have:

`x^3-2x^2-5x+10=0`

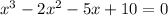
So, we can say that this equation comes from a function given by:

`f(x)=x^3-2x^2-5x+10`

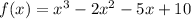
Thus, by plotting this function, we have that the graph of this function is indicated in Figure 1. By zooming, we can see, in Figure 2, that the roots of the polynomial equation are the x-intercepts of
`f(x)` which are:

`x_(1)=-2.236 \\ \\ x_(2)=2 \\ \\ x_(3)=2.236`

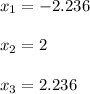
Finally, rounding noninteger roots to the nearest hundredth we have:

`\boxed{Root_(1)=-2.24} \\ \\ \boxed{Root_(2)=2} \\ \\ \boxed{Root_(3)=2.24}`

2. Using a system of equations.

The ordered equation is:

`x^3-2x^2-5x+10=0`

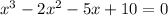
By arranging to factor out we have:

`x^3-5x-2x^2+10=0`

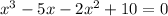
Then, by factoring:

`x(x^2-5)-2(x^2-5)=0`

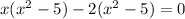
Term
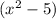`(x^2-5)` is a common factor, thus:

`(x-2)(x^2-5)=0 \\ \\ (x-2)(x-√(5))(x+√(5))=0 \\ \\ Finally: \\ \\ \boxed{Root_(1)=-√(5)=-2.24} \\ \\ \boxed{Root_(2)=2} \\ \\ \boxed{Root_(3)=√(5)=2.24}`