Question

The maximum displacement in an oscillatory motion is A = 0.49 m. Determine the position x at which the kinetic energy of the particle is half its elastic potential energy. (If KE = U/2 x= ?).​

Answer 1

x = 0.40 m

Step-by-step explanation:

• When the displacement is maximum, the particle is momentarily at rest, which means that at this point (assuming no friction present) all the mechanical energy is elastic potential, which can be written as follows:

`E_(tot) = U_(o) = (1)/(2) *k*A^(2) (1)`

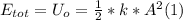
• Since in absence of friction, total mechanical energy must keep constant, this means that at any time, the sum of the kinetic and potential energy, must be equal to (1), as follows:

`E_(tot) = U_(o) = (1)/(2) *k*A^(2) = (KE)_(f) + U_(f) (2)`

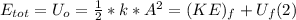
• If KEf = U/2f, replacing in (2), we get:

`E_(tot) = U_(o) = (1)/(2) *k*A^(2) = (U/2)_(f) + U_(f) = (3)/(2) *U_(f) (3)`

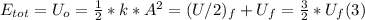
• At any point, the elastic potential energy is given by the following expression:

`U_(f) = (1)/(2) *k*x^(2) (4)`

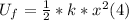
where k= spring constant (N/m) and x is the displacement from the

equilibrium position.

• Replacing (4) in (3), simplifying and rearranging, we get:

`E_(tot) = U_(o) = (1)/(2) *A^(2) = (3)/(4) *x^(2) (5)`

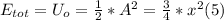
• Finally, solving for x, we get:

`x = \sqrt{(2)/(3) } * A = \sqrt{(2)/(3) } * 0.49m = 0.40 m (6)`