Answer:
θ = 83.6º
Step-by-step explanation:
- Once the shell is in the air, the only influence acting on it (assuming that the resistance of the air is negligible) is gravity.
- Gravity acts on the shell accelerating it in the vertical direction with a=g=-9.8 m/s2 (taking the upward direction as the positive one).
- Since movements in perpendicular directions are independent each other, we conclude that in the horizontal direction, speed must be constant.
- So, we can find the speed in the horizontal direction (the projection of the velocity vector along the horizontal axis) applying simply the definition of average velocity, as follows:
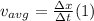
- Taking the launch site as the origin, and making the horizontal direction coincident with the x-axis (positive to the right), we know that the horizontal displacement is 81.7 m, and the time at the explosion, 8.6 s, so we can write the horizontal component of the velocity vector (its projection along the x-axis) as follows:
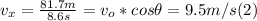
- In the vertical direction, since we know that the shell will explode when it reaches to the maximum height, at this point just before exploding, the vertical component of the velocity is just zero, even though it continues being accelerated downward.
- Applying the definition of acceleration, replacing a by the value of g, we can write the following expression:
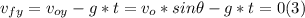
⇒ v₀* sin θ = g*t = 9.8m/s2* 8.6s = 84.3 m/s (4)
- Dividing (4) by (2), we can find tg θ (the angle of the initial velocity with the x-axis), as follows:
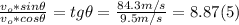
⇒ θ = tg⁻¹ (8.87) = 83.6º