Question

On the basis of a survey of 545 television viewers, a statistician has constructed a confidence interval and estimated that the proportion of people who watched the season premiere of Glee is between .16 and .24. What level of confidence (to the nearest percent, not a proportion) did the statistician use in constructing this interval

Answer 1

Confidence level of 98%.

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

Estimate:

The estimate
`\pi` is the mean of the two endpoints of the confidence interval. So

`\pi = (0.16+0.24)/(2) = (0.40)/(2) = 0.20`

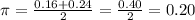
Survey of 545 television viewers

This means that
`n = 545`

What level of confidence (to the nearest percent, not a proportion) did the statistician use in constructing this interval

First we find z. The upper end is 0.24. So

`0.20 \pm z\sqrt{(0.2*0.8)/(545)} = 0.24`

`z\sqrt{(0.2*0.8)/(545)} = 0.04`

`0.017z = 0.04`

`z = (0.04)/(0.017)`

`z = 2.33`

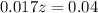
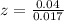
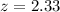
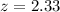`z = 2.33` has a pvalue of 0.99.

So

`1 - (\alpha)/(2) = 0.99`

`(\alpha)/(2) = 0.01`

`\alpha = 0.02`

`1 - \alpha = 1 - 0.02 = 0.98`

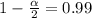
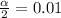
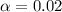
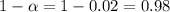
So a confidence level of 98%.