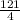Answer:
The value of c is
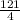
Explanation:
A perfect square trinomial is trinomial that can be written as the square of a binomial.
If,
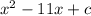 is a perfect square trinomial,
is a perfect square trinomial,
Then, we can write,
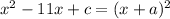 ---------(1)
---------(1)
Where a is any real number,
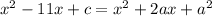 -------(2)
-------(2)
By comparing the coefficient of x,
We get,
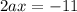
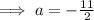
By substitution the value of a in equation (2),
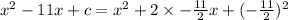
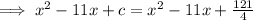
Again by comparing,
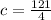
Hence, The value of c is