Question

What is the value of c such that x^2-11x+c is a perfect-square trinomial?

Answer 1

You can find what c is by completing the square.
y = x² - 11x +
`(121)/(4)` and this simplifies to (x -
`(11)/(2)`)²

So, c is
`(121)/(4)`

Answer 2

The value of c is
`(121)/(4)`

Explanation:

A perfect square trinomial is trinomial that can be written as the square of a binomial.

If,
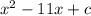`x^2-11x+c` is a perfect square trinomial,

Then, we can write,

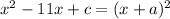`x^2-11x+c=(x+a)^2` ---------(1)

Where a is any real number,

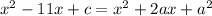`x^2-11x+c=x^2+2ax+a^2`-------(2)

By comparing the coefficient of x,

We get,

`2ax = -11`

`\implies a = -(11)/(2)`

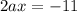
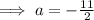
By substitution the value of a in equation (2),

`x^2-11x+c=x^2+2* -(11)/(2)x+(-(11)/(2))^2`

`\implies x^2-11x+c=x^2-11x+(121)/(4)`

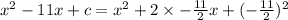
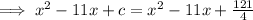
Again by comparing,

`c=(121)/(4)`

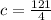
Hence, The value of c is
`(121)/(4)`