Question

I'm on my last question on a graded practice and I don't want to get a wrong. I have already graphed it.

Answer 1

c)rhombus

Step-by-step explanation

the slope of a line or segment is given by:

`\begin{gathered} slope=(y_2-y_1)/(x_2-x_1) \\ where \\ P1(x_1,y_1) \\ and \\ P2(x_2,y_2) \\ are\text{ the initial and end points} \end{gathered}`

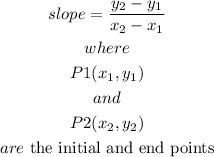
so

Step 1

find the slope of the given segments

a)slope of TU

let

`\begin{gathered} P1=T=(-2,7) \\ P2=U=(0,-2) \end{gathered}`

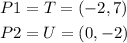
now, replace in the expression

`\begin{gathered} slope=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ slope=(-2-7)/(0+(-2))=-(9)/(2) \\ slope_(TU)=-(9)/(2) \end{gathered}`

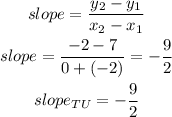
b) Slope of UV

Let

`\begin{gathered} P1=U=(0,-2) \\ P2=V=(7,-8) \end{gathered}`

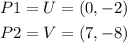
now, replace in the expression

`\begin{gathered} slope=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ slope=(-8-(-2))/(7-0)=(-6)/(7) \\ slope_(UV)=-(6)/(7) \end{gathered}`

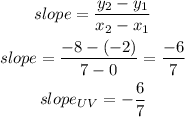
c)slope of VW

Let

`\begin{gathered} P1=V=(7,-8) \\ P2=W=(5,1) \end{gathered}`

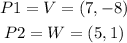
now, replace in the expression

`\begin{gathered} slope=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ slope=(1-(-8))/(5-7)=(9)/(-2) \\ slope_(VW)=-(9)/(2) \end{gathered}`

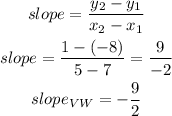
d) slope of WT

let

`\begin{gathered} P1=W=(5,1) \\ P2=T=(-2,7) \end{gathered}`

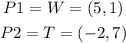
now, replace in the expression

`\begin{gathered} slope=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ slope=(7-1)/(-2-5)=(6)/(-7) \\ slope_(VW)=-(6)/(7) \end{gathered}`

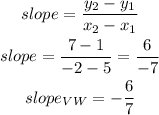
therefore, for the slopes the answer is

Step 2

lengths

the distance(d) between 2 points(P1 and P2) is given by:

`d=√((x_2-x_1)^2+(y_2-y_1)^2^)`

so

a) length of TU

let

`\begin{gathered} P1=T=(-2,7) \\ P2=U=(0,-2) \end{gathered}`

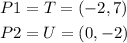
replace:

`\begin{gathered} d=√(\left(0-(-2\right))^2+(-2-7)^2) \\ d=√(4+81) \\ d_(TU)=√(85) \end{gathered}`

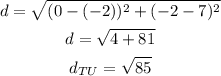
b) length UV

`\begin{gathered} d=√((7-0)^2+(-8-(-2))^2) \\ d=√(49+36) \\ d_(TU)=√(85) \end{gathered}`

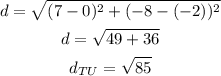
c)Length VW

`\begin{gathered} d=√((5-7)^2+(1-(-8))^2) \\ d=√(4+81) \\ d_(VW)=√(85) \end{gathered}`

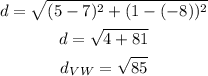
d)length WT

`\begin{gathered} d=√((5-(-2))^2+(1-7)^2) \\ d=√(49+36) \\ d_(WT)=√(85) \end{gathered}`

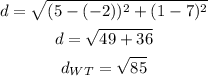
so

Step 3

finally, we have a parallelogram where all sides are equal, this is called

rhombus

I hope this helps you