Question

asked Apr 20, 2022 175k views

1 Answer

GegznaV · Answer 1 · 2022-04-24T08:40:51+0000

Answer:

a) 0.195 = 19.5% probability that exactly three arrivals occur during a particular hour.

b) 0.762 = 76.2% probability that at least three people arrive during a particular hour

c) 2 people.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

$P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)$

In which

x is the number of sucesses

e = 2.71828 is the Euler number

$\mu$ is the mean in the given interval.

Poisson process with a rate parameter of four per hour.

This means that
$\mu = 4$ .

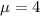(a) What is the probability that exactly three arrivals occur during a particular hour?

This is P(X = 3). So

$P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)$

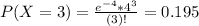
P(X = 3) = (e^(-4)*4^(3))/((3)!) = 0.195

0.195 = 19.5% probability that exactly three arrivals occur during a particular hour.

(b) What is the probability that at least three people arrive during a particular hour?

Either less than three people arrive during a particular hour, or at least three does. The sum of the probabilities of these outcomes is 1. So

$P(X < 3) + P(X \geq 3) = 1$

We want
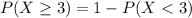$P(X \geq 3) = 1 - P(X < 3)$ , in which

P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) . So

$P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)$

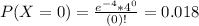
P(X = 0) = (e^(-4)*4^(0))/((0)!) = 0.018

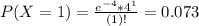
P(X = 1) = (e^(-4)*4^(1))/((1)!) = 0.073

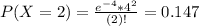
P(X = 2) = (e^(-4)*4^(2))/((2)!) = 0.147

So

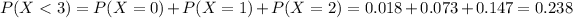
P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = 0.018 + 0.073 + 0.147 = 0.238

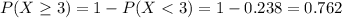
$P(X \geq 3) = 1 - P(X < 3) = 1 - 0.238 = 0.762$

0.762 = 76.2% probability that at least three people arrive during a particular hour.

c) How many people do you expect to arrive during a 30-min period?

One hour, 4 people

Half an hour = 30 min = 4/2 = 2 people.

Please log in or register to add a comment.